第55回(最終回)
アルゴリズムの基礎・5~バブルソート
最後尾から並べ替える~バブルソート連載の最後に、もう一度ソート――値の整列を試してみましょう。ちょっとひねった方法です。最後尾から比べていく本コラムの第51回で、数列の先頭から値を比較していく直接選択法を紹介しました。これは、並びの先頭の値を続く値と順次比較していくという、至極まっとうな方法でした。先のパズルで言えば、金貨を1枚ずつ取り出しては天秤で計る……というような感じで、仕組みは単純ですが手間がかかります。探索では、金貨を何枚かの組に分けたように、値の並びを中間値で二分することで、手間を減らすことができました。整列では、この手は使えません。そこで、値の比較を先頭からではなく最後尾から行うことを試してみます。 1つ前の値と比較する手順は次のようになります。
その1つ前の値と比較して、 比較元が小さければ値を入れ替えていく。 こうすることで、最も小さい値が並びの先頭に移動します。 次に、比較対象を最後尾から始めて先頭の次の次[3番目]まで繰り返します。すると、2番目に小さい値が並びの先頭に移動します。 カードで試してみるこのように、処理を1巡実行するたびに、比較対象の値は1個ずつ減っていきます。よって、同様の操作を「並びの数-1」回繰り返せば、すべての値が昇順に並びます。第51回でサンプルに含めたカードを使って、実際にテーブル上で試してみましょう。カードは図1のように並んでいます。 ※画面上でカードを並べ替えられるSilverlightアプリケーションを用意していますので、説明と合わせてお試しください。 » カード並べ替えアプリケーションを起動  図1:整列前のカード――第51回の図1と同じ 1巡目(図2)
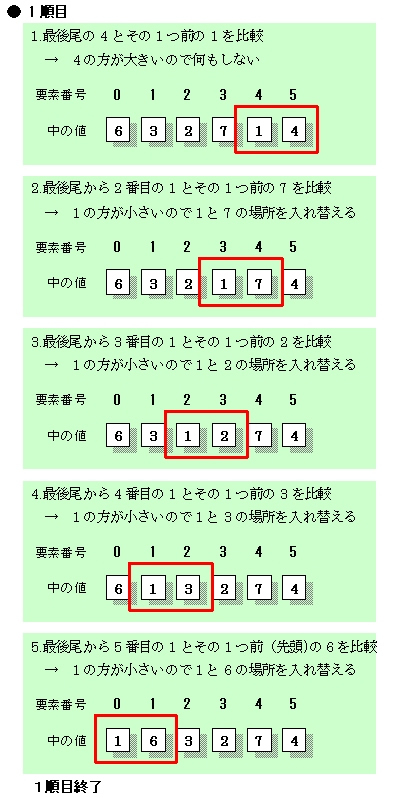 図2:並べ替えの1巡目 これで、最小値の「1」が列の先頭に移動しました。 2巡目
3巡目
4巡目
5巡目 この例では最後の2個の値「6と7」が昇順になっていますが、それは偶然でしかありません。
ボトムアップのバブルソートこの処理を眺めると、1巡目に1、2巡目に2……と、小さな数が順に前方に押し出されるように見えます。この様子が、泡が底から水面へと上がってくるように見えることから、この手法を「バブルソート」と呼びます。直接選択法が前方(項番号の若い方)から後方(項番号の多い方)へと視点を移動させるのに対して、バブルソートでは視点が後方から前方へと移動していきます。直接選択方はトップダウン・アプローチ、バブルソートはボトムアップ・アプローチということです。 |
Copyright © MESCIUS inc.