第51回
アルゴリズムの基礎・1~カードを使って整列(ソート)を実感しよう
基本の基本~数値の並べ替えでは、アルゴリズムの基本として、まず数値の並べ替え――ソートの手順を考えてみましょう。現実の問題として捉えてみよういきなり、大きな数値がたくさん存在する状況を前提にしてはいけません。コンピュータの処理だけではなく、あらゆる物事は単純化して捉えることで概要が見え、そこから仕組みや手順が明らかになっていくものです。まず、図1のように、それぞれ異なる1桁の数値が書かれた6枚のカードが、テーブルの上に並んでいるとします。 これを、値の小さい方から大きい方へ、左から右に並べ替えることにします。いわゆる「昇順のソート」です。 人間なら、瞬時に値の大小関係を見分け、図2のように並べ替えることができるでしょう。わざわざそのための手順を考える必要はありません。カードをぱっと見渡せば、1が最小、その次は2……と、ごく自然に判断できます。 しかし、コンピュータではそうはいきません。テーブル上のカードの群れをぱっと見渡すこともできなければ、手を動かしてカードを並べ替えることもできません。 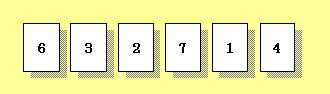 図1:バラバラに並んだ6枚のカード 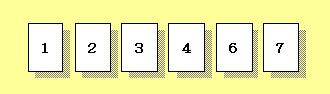 図2:左から小→大の順に並べ替えられたカード あなたがコンピュータになったら……?!数値の並びをコンピュータで処理するには、メモリの中に数値を配置し、それらに順番を表す番号を付けて管理しなければなりません。そして、それぞれの数値の大小関係を逐一判断しながら、順序を入れ替えていくことになります。あなたがコンピュータになったと想像して、この6枚のカードを並べ替える手順を考えてみましょう。 まず、最もシンプルな並べ替え方法を試してみます。それは、 とにかく、値の小さいカードを列の先頭(左端)に移動していく。という方法です。もう少し具体的にいうと、次のような手順になります。 カードの先頭から順に次(右側)の値と比較していく。 左側のカードより右側のカードの値が大きければ、 カードの位置を入れ替える。 この手順を、実際に試してみましょう。人間は目で見てカードの位置関係を瞬時に判断できますが、コンピュータでは各カード(数値)の位置を明確にするため、数値の入れ物を要素とした配列で扱う必要があります。そこで並んだ6枚のカードを、図3のように『0~5までの要素番号とその中の値』という形に置き換えてみます。 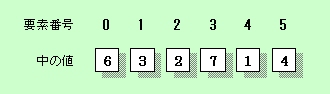 図3:カードの並びを要素番号とその中の値に置き換えてみる 手作業で並べ替えてみようここから、実際に6枚のカードで並べ替えの手順を試してみましょう(サンプル内にカードのPDFファイルが入っています)。※画面上でカードを並べ替えられるSilverlightアプリケーションはこちらからご利用いただけます。 ●1巡目
 図4:並べ替えの1巡目(0番が比較元) そして、比較元を先頭の次――2番目(1番)に移し、同様の操作を行います。 ●2巡目
さらに3番目(2番)と4番目(3番)とを比較……と、3巡目(図6)の操作を都合3回、4番目(3番)と5番目(4番)とを比較……と、4巡目(図7)の操作を都合2回、最後に5番目(4番)と最後尾の6番目(5番)とを比較する操作(図8)を1回行い、並べ替え操作は終了します。 先に、人間は瞬時に処理できると書きました。しかし、実は人間の頭の中でも上に掲げたような操作と似たような処理を行っています。ただ、それを無意識に行えるだけのことです。 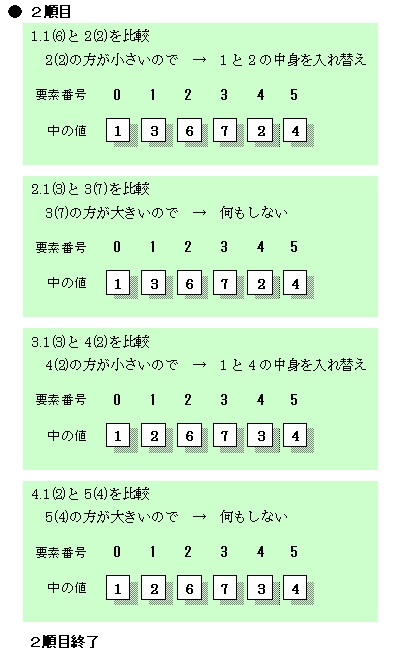 図5:並べ替え2巡目  図6:並べ替え3巡目 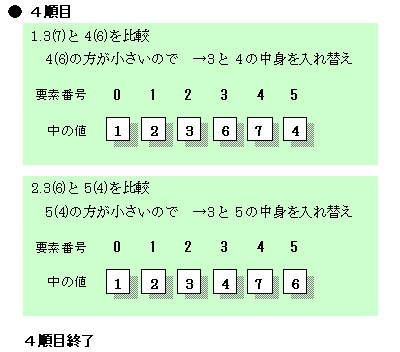 図7:並べ替え4巡目 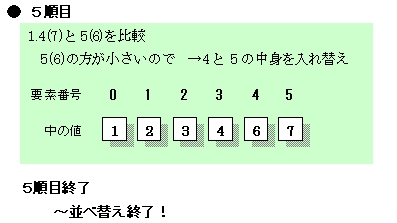 図8:並べ替え5巡目~並べ替え終了 |
Copyright © MESCIUS inc.