ビット演算子
表1にCのビット演算子を掲げておきます。ビット演算とは言っても、扱う値はバイト単位などCの一般的な整数のデータ型です。ビット演算子は、それらの値をビット単位で計算します。
ビットシフト演算(<< >>)~2倍と1/2
例えばunsigned char型の1は、2進数では"00000001"という形のビット列(ビットパターン)になります。これを1桁左にずらす(シフトする)と"00000010"となります。ずらしてあふれた左端の0は消え、空いた右端には0が入ります。
"00000001"は10進数の「1」、"00000010"は10進数の「2」です。つまり、ビット列を左に1桁シフトすると値は2倍になるのです。
逆に"00000010"(10進数の「2」)を右に1桁シフトすると"00000001"(10進数の「1」)──つまり元の値の1/2になります。このように、整数の値はビット列を1桁左右にシフトすることで簡単に2倍と1/2を計算できます(図1)。
さらに、2桁シフトすれば4倍、1/4倍、3桁シフトすれば8倍、1/8倍……と、2の累乗倍の計算が素早くできます。例えば
unsigned char x, y;
x = 50;
y = x << 2;
とすれば、変数yには200(50の4倍)が代入されます。
表1:ビット演算子
| 記号 |
機能 |
書式 |
説明 |
| << |
左シフト |
x << n |
xをn桁左シフト |
| >> |
右シフト |
x >> n |
xをn桁右シフト |
| ~ |
補数 |
~x |
xのビットパターンを反転 |
| & |
論理積 |
x & y |
xとyのビット単位の論理積 |
| | |
論理和 |
x | y |
xとyのビット単位の論理和 |
| ^ |
排他的論理和 |
x ^ y |
xとyとの排他的論理和 |
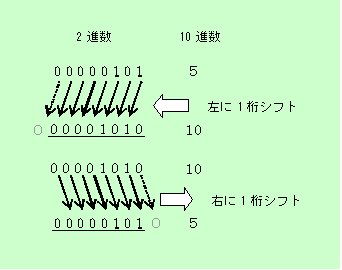 図1:符合なし整数は左に1桁シフトすると2倍に、右に1桁シフトすると1/2になる
ビットシフト演算(<< >>)~奇数倍
ビットシフトに加減算を組み合わせれば、3倍、5倍や1/3、1/5など奇数倍の計算もできます。例えば、変数xを1ビット左シフトしてそれにxの元の値を加算すればxの値は3倍に、2ビット左シフトしてxの元の値をを加算すればxの値は5倍に……ということになります。
unsigned char x, y;
x = 4;
tmp = x; -------- xの値を保持
y = x << 1; ----- yは8(4の2倍)
y += tmp; ------- yは12(8+4)
とすれば、変数yには12(4の3倍)が代入されます。
なお、これらビットのシフト演算ではunsigned──符合なし整数が前提となります。符合付きの整数では先頭ビットが符合(1=正 / 0=負)を表すため、上述のような結果にはなりません。
ビットの反転(~)
「~」記号で行うビットパターンの反転は、整数の補数を求めます。補数とは、加算するとすべてのビットがON(1)になる値です。
例えば"00000001"(10進数の1)の補数は"11111110"(10進数の254)です。両者を加算すると2進数では"11111111"になります。この値は10進数の255、16進数では"FF"(0xff)です。
つまり、ビット列を反転すると、符合なし整数では加算すると最大値、符合付き整数では-1になる――ということです。
ビットの論理積(&)
「&」記号によるビット単位の論理積とは、条件式で用いる論理演算の&&(論理積)を各ビット単位で行うものです。「両方が真なら結果は真/いずれか一方または両方が偽なら結果は偽」という計算を、各ビットごとに「両方がON(1)なら結果はON(1)/いずれか一方または両方がOFF(0)なら結果はOFF(0)」という形の演算を行います。
例えば、変数xが"01010110"で変数yが"00001000"のとき「x & y」の結果は"00000000"になります。変数xが"01011110"なら「x & y」の結果は"00001000"になります。
つまり、変数yの中でON(1)としたビットが変数xでもONならON、OFFならOFF──という具合に、ビットパターンの中の特定のビットがONかOFFかを調べられるということです(図2)。
また、特定のビットをOFFにすることも可能です。4ビット目 をOffにするなら"11110111 "という4ビット目だけ0であとは1の値(10進数の247 )との論理積を演算します。1との論理積は、元の値が0なら0、1なら1とそのままになり、0との論理積は必ず0になるからです。
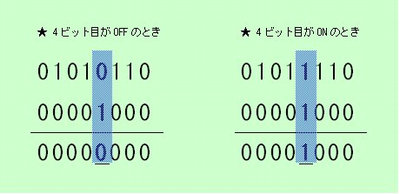
図2:ビット単位の論理積では特定のビットがONかどうかを調べられる
ビットの論理和(|)
「|」によるビット単位の論理和は、条件式で用いる論理演算の||(論理和)を各ビット単位で行うものです。「いずれか一方または両方が真なら結果は真/両方が偽なら結果は偽」という計算を、各ビットごとに「いずれか一方または両方がON(1)なら結果はON(1)/両方がOFF(0)なら結果はOFF(0)」という形の演算を行います。
例えば符号付き整数の演算では、変数yが"10000000"なら、「x | y」の結果は変数xの符号が負(−)になります。符号なし整数の演算では、変数yが"11111111"なら、変数xがどのような値であっても「x | y」の結果は必ず"11111111"(=符合なし整数の最大値)にできます。
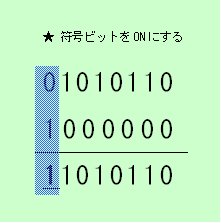 図3:ビット単位の論理和では特定のビットをONにできる
ビットの排他論理和(^)
「^」によるビット単位の排他的論理和では、双方の値が異なっているときだけ結果が1、双方の値が同じ場合には結果が0となります。
従って、同じ値同士を^で演算することによって、すべてのビットをOFF(0)にできます。「x ^ x」とすれば、xの値は必ず0になります。つまり、値のリセットです。これは「x = 0;」と、変数に0を代入しても同じ結果となりますが、アセンブリ言語では排他的論理和を使う方がマシンコードが短くなるためよく用いられます。
 図4:ビット単位の排他的論理和ですべてのビットをリセットできる
|